Геометрия 7 класс Отметил

Заранее

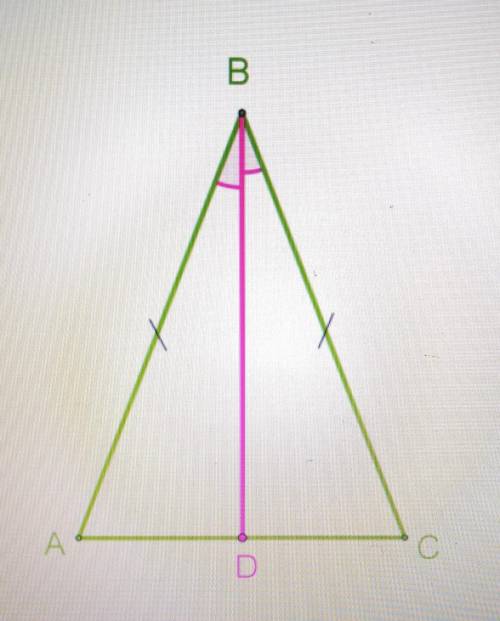
В равнобедренном треугольнике с длиной основании 51 проведена биссектриса угла ABCD. Используя второй признак равенства треугольника докажите, что отрезок BD является медианой, и определить длину отрезка AD.

Рассмотрим треугольники ΔABD и Δ__
(треугольник записать в алфавитном порядке);

1. так как прилежащие к основанию углы данного равнобедренного треугольника равны,
то ∡ A = ∡ __;

2. так как проведена биссектриса,
то ∡ __ = ∡ CBD;

3. стороны AB=CB у треугольников ΔABD и ΔCBD равны, так как данный
ΔABC — .

По второму признаку равенства треугольников ΔABD и ΔCBD равны.
Значит, равны все соответствующие элементы, в том числе стороны AD=CD. А это означает, что отрезок BD является медианой данного треугольника и делит сторону AC пополам.

AD= __ см

​

87074552993    1   02.12.2020 19:13    12