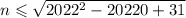 (где тама n - это N)
(где тама n - это N)
найти значение наибольшего натурального числа N, удовлетворяющего неравенству.
Другие вопросы по теме Математика
Популярные вопросы
- с башкирским кто сделает реально нкину еще балы...
3 - Как воспитывал герой в себе Робин Гуда? Приведите 3 конкретных примера из текста,...
1 - 10Кл1.На нейтралізацію 18,54 г α-амінокислоти витратили 40,32 г розчину лугу...
2 - Выполните 2 тестовых задания по Биологии за 10 класс. Буду благодарен за правильно...
3 - Вантажний автомобіль масою 5 т рухається рівномірно,коtфіwент сили тертя 0,023.Яку...
2 - . Масса осадка, выпавшего при добавлении 111 г 20% -го раствора хлорида кальция...
1 - Чему нас учит великое экологическое правило: Нельзя требовать от природы больше,чем...
2 - В шахматном турнире участвовало 15 учеников. Мальчиков было в 1,5 раза больше,...
2 - с физикой. Сколько колебаний происходит в электромагнитной волне с длиной волны...
2 - 1. Прочитайте диалог слепого и девушки-ундины ночью на берегу моря со слов...
2
Возведем правую и левую части неравенства в квадрат:
n² ≤ 4 088 484 - 20189
n² ≤ 4 068 295
✓(4 068 295) ≈ 2017,0015
ответ: наибольшее натуральное значение n, удовлетворяющее неравенство - 2017.