Функция y задана выражениями для различных областей изменения аргумента x . А) найти точки разрыва функции, если они существуют
Б) найти односторонние пределы и скачок функции в точках разрыва
В) построить график функции

Парабола  y=x²+1  чертится только для  х≤1 . Точка (1,2) принадлежит параболе .

Прямая у=3-х  проходит через точки (3,0)  и  (5,-2) . Точка (1,2) не принадлежит прямой, а точка (5,-2) принадлежит прямой .

Прямая  у= -3 параллельна оси ОХ и проходит через точку (0,-3) . Точка (5,-3)  не принадлежит этой прямой .

А) точка разрыва функции 1 рода - это х=5 , так как

Б)

Скачок функции в точке разрыва равен  

В)  График функции построен сплошными линиями .

P.S.  При х=1 функция непрерывна, так как левый и правый пределы функции в этой точке равны между собой и равны значению функции в точке х=1 :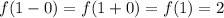    .