Функция убывает на всей числовой оси

4

Пошаговое объяснение:

Производная этой функции равна

Чтобы функция убывала на всей числовой оси, неравенство f'(x) < 0 должно выполняться для любого x. Заметим, что -eˣ < 0 при любом x. Тогда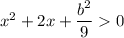 . Это парабола, ветви направлены вверх. Она не имеет корней, а значит, лежит выше оси Ox, если дискриминант отрицателен: 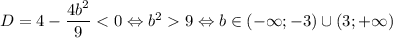. Минимальное натуральное b, подходящее условиям — 4.