F(x)=(3-2x)^2-4mx+4m при каком значении параметра m функция является чётной?
Другие вопросы по теме Математика
Популярные вопросы
- Iam laying in bed или i am lying on bed как правильно ? и почему...
1 - Два соединены паралельно и подключены к источнику тока. эдс источника тока...
2 - Нужно: два мальчика собрали 420 комиксов у одного оказалось га 10 % больше...
3 - Подбери проверочное слово , затем впиши нужную букву....
3 - А. п. чехов на мельнице краткое содержание. !...
2 - Каким методом воспользовался и. п. павлов чтобы установить рефлекторную природу...
1 - А.п. чехов смерть чиновника . краткое содержание, ....
2 - На материальную точку одновременно действуют две силы. f1=3,f2=4.определите...
2 - Значение какого фразеологизма объяснено неверно седьмая вода на киселе-дальний...
3 - Три фактора влияющие на формирование спроса,проиллюстрировать их в конкретном...
3
ответ: m = -3
Пошаговое объяснение:
Функция является четной, если выполняется равенство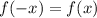
При m=-3 получится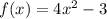 — четная.
— четная.