F(x)=1-x^3+2ax^2-4ax при каких значениях параметра а функция убывает на все числовой прямой

Question

Математика: F(x)=1-x^3+2ax^2-4ax при каких значениях параметра а функция убывает на все числовой прямой

skrlp1234 · Answer

F(x)=1-x^3+2ax^2-4ax

Функция убывает при отрицательном значении производной (также допускается равенство нулю производной в отдельных точках, но не на сплошном интервале). Находим производную:

F'(x)=-3x^2+4ax-4a

Необходимо потребовать, чтобы производная функции была неположительна:

$-3x^2+4ax-4a\leq0$

Поскольку уравнение имеет отрицательный старший коэффициент, то неравенство будет выполняться для всех х при неположительном дискриминанте:

$D=(4a)^2-4\cdot(-3)\cdot(-4a)=16a^2-48a \\\ 16a^2-48a\leq0 \\\ 16a(a-3)\leq0$

Решая неравенство по методу интервалов, получим:

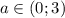$a\in[0;3]$

При $a\in(0;3)$ производная будет строго отрицательной, при а=0 и а=3 производная будет равняться нулю в отдельной точке. Во всех этих случаях исходная функция убывает на всей числовой прямой

ответ: $a\in[0;3]$

F(x)=1-x^3+2ax^2-4ax при каких значениях параметра а функция убывает на все числовой прямой

Популярные вопросы