Это задание было сегодня на ЕГЭ(2021)
понять правильно я его сделала или нет
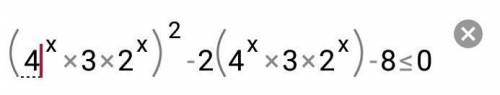
Другие вопросы по теме Математика
Популярные вопросы
- Как называются машини которые режут камни,черпают землю,режут...
2 - 5 48 на сколько одно число больше другого...
3 - Имя основателя династии российских царей...
3 - Подчеркни правильный вариант. 3)my rubber is in my pencil/ pen/...
1 - Запишите дробь 0,035; в виде несократимой обыкновенной дроби...
3 - Какие слова професионализмы употребляют только журналисты? !...
1 - Проверочное слово к слову проявление...
3 - Два поезда идут навстречу друг другу со скоростями 36 и 54 км/ч....
2 - Всегда ли положительное влияние технического прогресса на окружающую...
2 - Умаши и даши было поровну конфет. маша отдала даше две конфеты....
3
4^x*3*2^x = 2^2x * 3 * 2^x = 3*2^3x
(3*2^3x)^2 - 2*(3*2^3x) - 8 ≤ 0
3*2^3x = z > 0
z² - 2z - 8 ≤ 0
D = 4 + 32 = 36
z12 = (2 +- 6)/2 = 4 -2
(z + 2)(z - 4) ≤ 0
[-2] [4]
z∈ (-∞, -2] U [4, + ∞)
1. z ≥ -2
x ∈ R
2. z ≤ 4
3*2^3x ≤ 4
2^3x ≤ 4/3
3x ≤ log(2) 4/3
x ≤ (log(2) 4/3)/3 = (log(2) 4 - log(2) 3)/3 = (2 - log(2) 3)/3
x ∈ ( -∞. (2 - log(2) 3)/3)