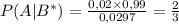Есть редкое заболевание, которое встречается у 1% населения. Есть тест, который дает положительный результат на 99% больных людей и ложный положительный результат на 2% здоровых людей. Тест показывает положительный результат на пациента. Какова вероятность того, что у пациента нет заболевания?
Другие вопросы по теме Математика
Популярные вопросы
- Начни читать текст. по сигналу учителя поставь палочку после того слова, до...
1 - Номер в отеле стоит 120$ за сутки в течение первой недели пребывания. каждые...
3 - Что такое качество печати принтера?...
2 - Найдете наибольшее и наименбшее целыесли решения неравенства l5+9хl 20 -(знак...
1 - Какие нужно ставить знаки препинания? у арктики есть много необычных явлений...
2 - Площадь второго круга составляет 0,25 площади первого круга.найдите площадь...
3 - Пересекает ли окружность луч началом в центре окружности (o,r) ? если пересекает...
1 - A)присоединение казани б)взятие измаила в)бородинская битва. 1)михаил кутузов....
2 - Утворити форми слова і підібрати спільнокоренневі слова від слів : великий,небо,сміх...
3 - Какую подделку можно подарить на 23 февраля. пришлите фото...
2
Назовем событие — человек здоров, событие
— человек здоров, событие 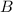 — болен, событие
— болен, событие 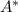 — здоров согласно результатам теста,
— здоров согласно результатам теста,  — болен согласно результатам теста. Нам требуется определить величину
— болен согласно результатам теста. Нам требуется определить величину 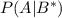 .
.
По теореме Байеса: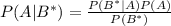 .
.
При этом ,
,  ,
,  .
.
Вероятность того, что обследование показало, что человек болен, то есть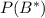 , складывается из двух вероятностей: человек болен и это показало обследование и человек здоров, и имеет место ложноположительный результат. То есть
, складывается из двух вероятностей: человек болен и это показало обследование и человек здоров, и имеет место ложноположительный результат. То есть 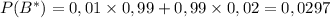 . Итак,
. Итак,