Есть 30 карточек (синих и красных). числа на синих карточках натуральны и различны, любое число на синей карточке больше любого числа на красной. среднее арифметическое чисел на всех карточках равно 12. все числа на синих карточках увеличили в 5 раз, среднее арифметическое стало равно 52. а) могло ли быть 10 синих карточек? б) могло ли быть 10 красных карточек? в) какое наибольшее количество синих карточек могло быть?

Ответы

olyacuznet5ova 09.07.2020 15:17

«Любое число на синей карточке больше любого числа на красной» означает, что минимальное число среди синих карточек больше наибольшего числа среди красных карточек.

Пусть сумма чисел на синих карточках равна S₁, сумма чисел на красных – S₂. Тогда по условию получаем, что:

$\left \{ {{\frac{S_{1}+S_{2}}{30}=12} \atop {\frac{5S_{1}+S_{2}}{30}=52}} \right. \left \{ {{S_{1}+S_{2}=360} \atop {5S_{1}+S_{2}=1560}} \right. \Rightarrow S_{1}=300, S_{2}=60$

а) Попробуем составить пример, чтобы сумма 20 чисел на красных карточках составляла 60 (числа необязательно различны): возьмём все по 3. Если среди синих взять числа от 4 до 13, то их сумма составит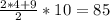 $\frac{2*4+9}{2}*10=85$ . Если к последнему числу прибавить 215, то сумма чисел на синих карточках как раз составит 300. Итак, если на красных карточках взять числа по 3, а на синих – 4, 5, 6... 11, 12, 228, то все условия выполнятся. Значит, такое может быть.

б) Если красных карточек 10, то синих – 20. Чтобы максимальное число на красных карточках было минимальным, нужно взять все числа равными, то есть по 6. Синих карточек получается довольно много, поэтому имеет смысл проверить их минимально возможную сумму. Эта сумма равна 7 + 8 + 9 + ... + 26, или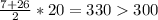 $\frac{7+26}{2}*20=330300$ , значит, сумму 300 на синих карточках мы получить не сможем, то есть такого быть не может.

в) По пункту б) 20 синих карточек быть не может, а с увеличением числа синих карточек их минимально возможная сумма возрастает. Значит, их не более 19.

Если их 19, то красных – 11. Тогда среди красных минимально возможное наибольшее – 6 (6*9 + 5 + 1 = 60). Минимально возможная сумма на синих карточках

$\frac{7 + 25}{2} \times 19 = 304 300$