Если множеством решений неравенства ax^2+bx +c > 0 является интервал (3; +∞), то (a+c)/b=

Если для некоторого неравенства вида ах²+bх+с > 0 множеством решений является открытый луч (3; +∞), то параметр а = 0.

Тогда получаем, что bх+с > 0, откуда при b>0 следует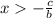

Запись (3; +∞) равносильна неравенству x > 3.

Тогда при b>0 имеем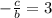 , т.е. с=-3b

Теперь получим: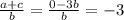

ответ: -3