ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ, ОЧЕНЬ ЛЕГКО! Задание на скриншоте.
Можно без решения (только ответ), но если не сложно )
За бессмысленные или не правильные ответы жалоба
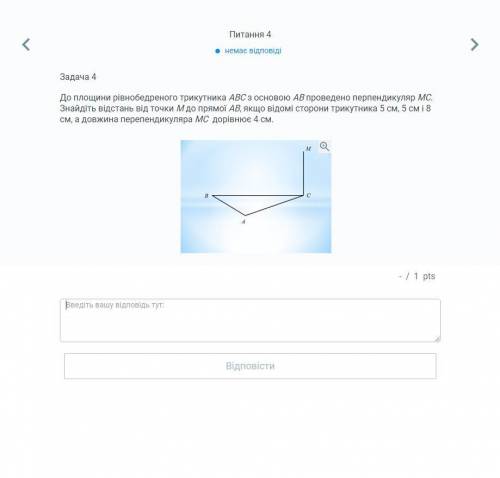
Другие вопросы по теме Математика
Популярные вопросы
- Отметь трёхсложное слово с ударением на 2-м слоге. азбука,гитара,водопад,карман,...
1 - Выразите в дециметрах 50см 230см 67м 800м...
3 - Угадайте закономерность и заполните пропуски а)ii iv vi б)i iii v ix...
3 - Сочинение на тему: нужна ли строителю дорог?...
3 - 4003, 4030 , ! в каком числе 40сотен...
2 - Проведите фонетический разбор слова недооценка...
3 - Огород имеет форму прямоугольника! длина одной его стороны 32 метра.а...
1 - Составьте буквенное выражение частное числа 25 и суммы чисел х и у ,...
1 - При живых организмов,в телах других живых организмов?...
1 - Запишите выражение и найдите его значение: а)сумма квадратов чисел -3...
3
5 см
Пошаговое объяснение:
IACI=IBCI по условию, как стороны равнобедренного треугольника.
Построим отрезок СN такой, что IANI=IBNI. Отрезок CN является одновременно медианой, высотой и биссектрисой, опущенной на основание равнобедренного треугольника. Следовательно ∠CNA = ∠CNB = 90° (по определению высоты, опущенной из вершины на основание), и IANI=IBNI (по определению медианы).
Плоскость ΔMNC перпендикулярна отрезку AB, т.к. AB ⊥CN (определение: прямая перпендиклярна плоскости, если она перпендикулярна любой прямой, принадлежащей плоскости), следователно и MN ⊥ AB.
Следовательно длина отрезка IMNI и есть расстояние от точки M до стороны (отрезка) AB (определение: расстояние от точки до плоскости есть длина перпендикуляра, опущенного из точки на плоскость).
Найдем длину отрезка MN:
1. Сначала найдем длину ICNI:
ICNI=√(IBCI² - INBI²);
ICNI=√(5²-4²)=√9=3;
2. А теперь найдем IMNI из ΔMNC:
IMNI=√(ICNI²+ICMI²);
IMNI=√(3²+4²)=√25=5 (см)