Двойной интеграл в полярных координатах. Не могу определить пределы интегрирования, учитывая, что центр круга смещен решить .

Двойной интеграл в полярных координатах. Не могу определить пределы интегрирования, учитывая, что це

Ответы

Прунчик1056 11.08.2021 02:42

D ограничена окружностью $(x-\frac{1}{2})^2+(y-\frac{1}{2})^2=\frac{1}{2}$

c центром в точке M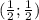 $(\frac{1}{2};\frac{1}{2})$ и радиусом 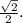$\frac{\sqrt{2}}{2}.$ Можно или сначала сделать сдвиг x-1/2=u, y-1/2=v, а потом ввести полярные координаты, или объединить эти две операции в одну. Естественно, модуль якобиана перехода будет равен r, как и в случае обычного перехода к полярной системе. Итак,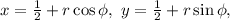 $x=\frac{1}{2}+r\cos \phi,\ y=\frac{1}{2}+r\sin \phi,$

$I=\int\limits_0^{2\pi}d\phi\int\limits_0^{1/\sqrt{2}}r(\frac{1}{2}+r\cos\phi+\frac{1}{2}+r\sin\phi)\, dr;$

если разбить на отдельные интегралы, интегралы от слагаемых с косинусом и синусом обнулятся (как любой уважающий себя интеграл от синуса или косинуса по промежутку длиной в период или несколько периодов) и останется только интеграл

$\int\limits_0^{2\pi}d\phi\int_0^{1/\sqrt{2}}r^2\, dr=2\pi\frac{r^3}{3}|_0^{1/\sqrt{2}}=\frac{\pi\sqrt{2}}{6}.$

Замечание. Если кто-то не любит комфорт, можете просто перейти к полярным координатам, но тогда угол будет меняться от минус пи/4 до 3 пи/4, а полярный радиус от нуля до косинус фи плюс синус фи.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика