1. Математика
  2. Двое Трактористов работая

Двое Трактористов работая вместе могут вспахать поле за 4 дня. Если первый трактор вспашет 1/3 поля, а затем его заменит второй, то всё поле будет вспахано за 10 дней. За сколько дней может вспахать поле каждый тракторист, работая самостоятельно, если первый работает медленнее

​

pelmenev777 pelmenev777    1   06.05.2020 14:54    11

Ответы
olmilevskaya1 olmilevskaya1  14.10.2020 08:43
Решение:Пусть x - это та часть поля, которую вспахивает 1-ый тракторист за 1 день, а y - та часть поля, которую вспахивает уже 2-ой тракторист, но тоже за 1 день.

Мы можем составить систему уравнений!

За 4 дня первый тракторист вспашет 4x части поля, а второй - 4y части поля. И, по условию, сумма этих двух чисел равна 1 (полю).Время, за которое 1-ый трактор вспашет 1/3 поля составляет (1/3)/x, а то время, за которое второй трактор вспашет 1-1/3=2/3 поля равно не иначе, как (2/3)/y. И сумма этих двух отрезков времени - 10 дней.

Есть две переменных - но и есть два уравнения:

\displaystyle \left \{ {{4x+4y=1} \atop { \frac{(1/3)}{x} + \frac{(2/3)}{y}=10 }} \right. ;    \displaystyle \left \{ {{4y=1-4x} \atop { \frac{1}{3x} + \frac{2}{3y} = 10}} \right. ;    \displaystyle \left \{ {{y = 0,25-x} \atop {3y+6x=90xy}} \right. .

Можем сделать подстановку:

3 \cdot (0,25-x) + 6 \cdot x = 90 \cdot (0,25-x) \cdot x

0,75+3x=22,5x-90x^2

90x^2-19,5x+0,75=0

120x^2-26x+1=0

Дальше, воспользовавшись формулой корней полного квадратного уравнения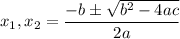 x_1,x_2=\dfrac{-b \pm \sqrt{b^2-4ac} }{2a}, получим:

x_1=\dfrac{1}{20} , \;\;\; x_2 = \dfrac{1}{6} .

Осталось только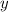 y-и найти:

\displaystyle y_1=0,25- \frac{1}{20} = \frac{1}{5} \\\\y_2=0,25-\frac{1}{6} = \frac{1}{12}

Итак, у нас есть два решения, и между ними придется сделать выбор.

По условию дано, что " ... первый работает медленнее ... ". Это означает, что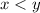 x < y.

Но под этот критерий подходит только первое решение (так как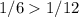 1/6 1/12):

\displaystyle \left \{ {{x_1=\frac{1}{20} } \atop {y_1=\frac{1}{5} }} \right.

Если мы сделаем проверку, то это решение будет удовлетворять всем условиям.

Но все же заметим, что пока ответа задачи у нас нет. Так что самое время его получить.

\displaystyle t_1 = \frac{S}{v_1} = \frac{1}{\frac{1}{20} } = 20 (дней)

\displaystyle t_2 = \frac{S}{v_2} = \frac{1}{\frac{1}{5} } = 5  (дней)

Задача [наконец] решена!

ответ:

первый тракторист может вспахать поле за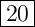 \Large { \boxed {20} } дней,

а второй - за \Large { \boxed {5} } дней.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
liza45683liza liza45683liza  30.09.2019 11:10
Корень из 98 умножить на корень из 16 разделить на корень из 50...
lagis9 lagis9  30.09.2019 11:10
Сумма 9 одинаковых по массе сплавов равна 8 кг .напишите массу 1 сплава...
Petrosyaniha Petrosyaniha  30.09.2019 11:10
Техника выполнения специально беговых кратко...
АннаФилип270406 АннаФилип270406  30.09.2019 11:10
Вдвух шкафах было 1000 книг когда из одного шкафа взяли 147 книг а из другого 49 книг то в обоих шкафах книг осталось поровну сколько книг осталось в каждом шкафу...
катя5069 катя5069  30.09.2019 11:10
Предмет обихода 4 буквы последняя с...
bosschornoguz bosschornoguz  30.09.2019 11:10
Спортсмен бежит со скоростью 420м/мин. сколько метров он пробежит за: a)2 минуты b)1,45 минуты c)3 минуты 18 секунд решить...
никита3447 никита3447  30.09.2019 11:10
Реши с уравнения: в классе было несколько учеников.после того как 7 учеников вошли и 9 вышли,в классе их стало 31.сколько учеников было в классе первоначально?...
VikaPikcha VikaPikcha  30.09.2019 11:10
Площадь участка земли прямоугольной формы 720м² длина участка -24м вычисли его ширину и периметр участка...
mira132 mira132  30.09.2019 11:10
Моторний човен пройшов за течією річки і повернувся у початковий пункт. швидкість течії річки дорівнює 3 км/ год, а швидкість човна у стоячій воді 15 км/год .на яку відстань від...
maina342 maina342  30.09.2019 11:10
Решить в столбик (3000+240): 10=? решить надо в столбик деление...

Популярные вопросы