Две студенческие бригады могут выполнить задание, работая вместе 6ч. За сколько часов может выполнить это задание каждая бригада, работая самостоятельно, если одной из них для выполнения 2/5 задания нужна на 4 часа больше, чем другой для выполнения 1/5 задания.
Другие вопросы по теме Математика
Популярные вопросы
- Доклад о политической партии россии план: программа (самое важное) создания...
3 - Установите соединения между классом соелиненен й и тривиальном названием...
2 - Всередине 19 века в сша действовала подземная железная дорога , которая переправляла...
3 - При повреждении вены конечности необходимо...
3 - Что вы знаете о возвышенных равнинах...
1 - Вданный момент обыкновенная акция имеет курсовую стоимость 20 тыс. руб.,...
2 - Напиши, почему тебе нравятся ёлочки...
3 - Составь предложения со словами нарезать наклеить налепить...
1 - Сталь вова собираться школу.списать,вставляя предлоги...
2 - Complete the sentences in reported speech john said i love this school john...
3
Если всю работу взять за 1.
Пусть первая бригада выполнит 1/5 задания за х часов
тогда вторая бригада за х+4 часа
Производительность труда при работе вместе бригад равна 1/6
Производительность первой бригады будет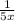
производительность второй бригады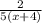
Исходя из этого получаем уравнение
Пошаговое объяснение: