Две подруги Катя и Марьяна задумались о том, как рассчитать площадь поверхности зонта.
На первый взгляд зонт кажется
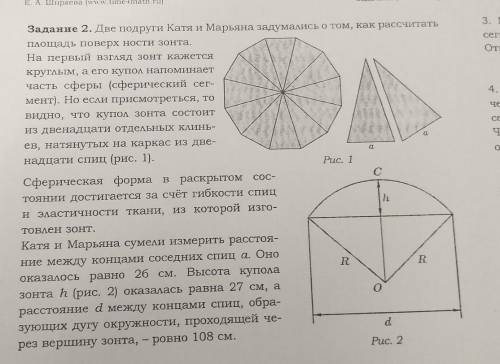
круглым, а его купол напоминает
часть сферы (сферический сегмнет). Но если присмотреться, то видно, что купол зонта состоит из двенадцати спиц. (рис 1)​

Привет!

Для того чтобы рассчитать площадь поверхности зонта, мы должны разбить его на более простые геометрические фигуры, для которых мы уже знаем формулы для расчета площади.

Если мы взглянем на зонт, то можем заметить, что его купол состоит из двенадцати равных сегментов или спиц. Каждая из этих спиц похожа на треугольник. Давай-ка разберемся, как их посчитать!

Шаг 1: Рассчитаем площадь одного сегмента.
Каждый сегмент похож на изогнутый конус. Чтобы найти площадь поверхности конуса, нужно использовать формулу: S = π * r * l, где S - площадь, r - радиус основания конуса, а l - образующая конуса (измеряется от центра основания до вершины конуса).

У нас есть радиус основания конуса (это радиус зонта), но нам нужно найти образующую конуса. Для этого давай-ка воспользуемся теоремой Пифагора в треугольнике.

Шаг 2: Найдем высоту треугольника (образующую конуса).
Высота треугольника - это отрезок, соединяющий центр окружности (середину основания зонта) с вершиной треугольника (вершина спицы). Мы можем найти высоту, используя формулу Пифагора: h^2 = c^2 - a^2, где h - высота, c - образующая конуса, а a - радиус основания конуса.

Теперь, используя найденную высоту и радиус основания, мы можем рассчитать образующую конуса.

Шаг 3: Найдем площадь сегмента.
Теперь, когда у нас есть радиус основания и образующая конуса, мы можем использовать формулу для площади поверхности конуса и умножить ее на 2, чтобы получить площадь одного сегмента зонта.

Шаг 4: Найдем площадь поверхности зонта.
Наконец, чтобы найти площадь поверхности зонта, мы умножаем площадь одного сегмента на 12 (потому что у нас 12 спиц) и получаем окончательный ответ.

Вот таким образом мы можем рассчитать площадь поверхности зонта, разбив его на более простые геометрические фигуры и используя соответствующие формулы для расчета площади.