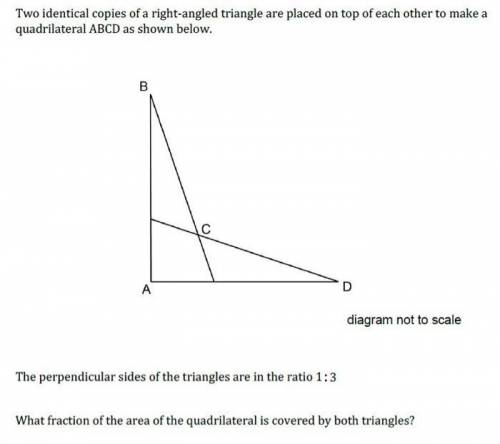
Две идентичные копии прямоугольного треугольника помещаются друг на друга, чтобы получился четырехугольник ABCD, как показано ниже. B С A D диаграмма не в масштабе Перпендикулярные стороны треугольников находятся в соотношении 1: 3 Какая часть площади четырехугольника покрыта обоими треугольниками?

ответ: 5/7

Пошаговое объяснение:

Проведем перпендикуляр RG  к cтороне AB. Поскольку стороны перпендикулярных сторон относятся как 3:1, то обозначим доли отношений: BR =TD = 2x; AR = AT= x.

Откуда Δ ABT подобен Δ RBG, а значит:

RG = 2x/3

Δ CRG подобен Δ CTD по двум накрест лежащим углам при параллельных прямых, а значит:

GC/CT = RC/CD = (2x/3)/2x = 1/3

Тогда:

RD/CD = 4:1

Заметим, что  Δ RAD и Δ СTD имеют общий угол при вершине D. Площади обоих треугольников можно найти следующим образом:

S Δ RAD = 0.5*RD*AD*sinD

S Δ CTD = 0.5*CD*TD*sinD

Откуда:

S Δ RAD/S Δ CTD = (RD*AD)/(CD*TD) = (RR/CD) * (AD/TD) =4 * 3/2 = 6

Обозначим: S Δ RAD = S ΔBAT = S, тогда:

S Δ CTD = S Δ BRC = S/6

Таким образом, можно выразить площадь четырехугольника покрытого обоими прямоугольными треугольниками:

S RCTA = S - S/6 = 5S/6

Теперь найдем площадь четырехугольника ABCD:

S ABCD = 2S/6 + 5S/6 = 7S/6

Наконец получаем:

S RCTA/S ABCD = 5/7

S RCTA = (5/7) * S ABCD