Два треугольных участка земли подобны друг другу. Стороны одного участка 56 метров, 45 метров и 38 метров. Средняя сторона второго участка 247,5 метров. а) Вычислить стороны второго участка. б) Во сколько раз отличаются периметры участков? (показать вычисления).​

ответ:  308 м.  209 м.  В 5,5 раз.

Пошаговое объяснение:

Дано. Первый треугольник ABC, у которого АВ=56 м, ВС=45 м и АС = 38 м. Второй треугольник А1В1С1  подобен АВС (по условию). Найти стороны второго участка.

Решение.

 Найдем коэффициент подобия треугольников:

k=В1С1/ВС=247,5 : 45 = 5,5.  Тогда

А1В1 = 56*5,5 = 308 м.

А1С1 = 38*5,5 = 209 м.

Периметр Р= 56+45+38 = 139 м.

Периметр  Р1=247,5+308+209=764,5‬ м

Р1/Р = 764,5‬ : 139 = 5.5

В 5,5 раз  - на коэффициент пропорциональности.

а) 308 м, 247,5 м, 209м

б) В 5,5 раз.

Пошаговое объяснение:

а) Раз треугольники подобны, то их стороны по определению пропорциональны.

Давайте для наглядности обозначим эти два треугольника буквами : первый пускай будет △ABC, а второй — △DEF. В таком случае можно сделать такую запись: △ABC ~ △DEF (знак тильда должен находиться на уровне букв).

Теперь составляем такую запись :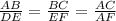  

Подставляем известные стороны :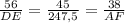  

И вычисяем две неизвестные стороны второго треугольника :

1 :  

м

 м

2 (через коэффициент пропорциональности) :

м

м

ответ : Остальные две стороны второго треугольника равны 308 м и 209 м.

б) P(△ABC) = 45 + 56 + 38 = 139 м

P(△DEF) = 308 + 247,5 + 209 = 764,5 м

ответ : Периметры участков отличаются в 5,5 раз (тот же коэффициент пропорциональности).