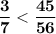Дроби к общему знаменателю и сравните их: 3/4 и 11/12, 4/5 и 7/15, 1/6 и 13/24, 3/7 и 45/56

Чтобы привести дроби к общ. знаменателю, найдем НОЗ. Для этого разложим числа в знаменателях на множители. Возьмём множители большего числа и умножим на недостающие множители второго числа.

========================

Например,

4 = 2 * 2

12 = 3 * 2 * 2

А т.к. в множителях числа 12 есть и множители числа 4, то просто перемножим множители 12 и получим НОЗ.

3 * 2 * 2 = 12 - НОЗ

Приведем к общ. знаменателю

У дробей с одинаковыми знаменателями сравниваются числители, соответственно если числитель больше, то и дробь больше, а если числитель меньше, то и дробь меньше.

            ⇔        

***************************************

Дальше.

5 - простое число, т.е. 5 = 1 * 5

15 = 3 * 5

Найдем НОЗ

3 * 5 = 15 - НОЗ

Приведем к общ. знаменателю

       ⇒            ⇔    

***************************************

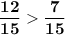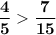
6 = 2 * 3

24 = 2 * 2 * 2 * 3

Найдем НОЗ

2 * 2 * 2 * 3 = 24 - НОЗ

Приведем к общ. знаменателю

        ⇒           ⇔      

***************************************

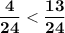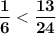
7 - простое число, т.е. 7 = 1 * 7

56 = 2 * 2 * 2 * 7

Найдем НОЗ

2 * 2 * 2 * 7 = 56 - НОЗ

Приведем к общ. знаменателю

        ⇒         ⇔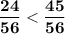