Довести що число 1³+2³+...+9³не ділиться на 10​

Пошаговое объяснение:

Рассмотрим остатки при делении на 10 данных чисел (просто последняя цифра)

1³ = 1 => 1

2³ = 8 => 8

3³ = 27 => 7

4³ = 64 => 4

5³ = 125 => 5

6³ = 216 => 6

7³ = 343 => 3

8³ = 512 => 2

9³ = 729 => 9

Сложим все эти остатки

1 + 8 + 7 + 4 + 5 + 6 + 3 + 2 + 9 = (1 + 9) + (8 + 2) + (7 + 3) + (4 + 6) + 5 = 10 + 10 + 10 + 10 + 5 = 45

остаток при делении 45 на 10 это 5.

Так как 5 не равно 0, значит исходное выражение не делится на 10 по свойству остатков

Для любого натурального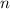 имеет место следующее равенство

Это равенство можете доказать самостоятельно с метода математической индукции.

Для n = 9: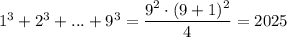 не делится на 10.