1. Математика
  2. Доведіть що рівняння x4

Доведіть що рівняння x4 – 4x3+ 12x2 – 24x +24=0 не має розвязків

AlexLLG AlexLLG    1   22.05.2019 09:10    0

Ответы
kofhagje46 kofhagje46  17.06.2020 13:52

x^4-4x^3+12x^2-24x+24=0;\\\\x^4-4x^3+4x^2+8x^2-24x+24=0;\\\\x^2(x^2-4x^2+4)+8(x^2-3x+3)=0;\\\\x^2(x-2)^2+8(x^2-3x+3)=0

 

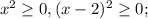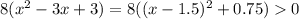
при будьякому дійсному  х: x^2 \geq 0, (x-2)^2 \geq 0; а 8(x^2-3x+3)=8((x-1.5)^2+0.75)0

л.ч. представляє собою суму двох добутків, перший з яких невідємний (як добуток двох невідємних множників), другий додатній як добуток двох додатніх, тому л.ч. при будьякому дійсному х додатня, а значить дане рівняння не має розвязків (л.ч. зажди більша за 0)

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
vladyslav2523 vladyslav2523  08.06.2019 23:50
Ятуплю. люди я забыла первый класс как умножить дробь с одинаковым числителем и знаминателем 1/10 evyj; bnm yf 1/10...
carollabelle carollabelle  08.06.2019 23:50
Вначале учебного года в школе было 1440 учащихся, а к концу года их стало 1728. на сколько процентов увеличилось за учебный год число учащихся?...
liliasirbu liliasirbu  08.06.2019 23:50
Втреугольнике авс отмечены середины м и n сторон вс и ас соответственно . площадь треугольника смn =2 . найти площадь четырёхугольника авмn...
superrada superrada  08.06.2019 23:50
Расстояние между пристанями а и в равно 48 км из а и в по течению реки отправился плот а через час вслед за ним отправилась моторная лодка, которая, прибыла в пункт в, тотчас повернулась...
myafyanya myafyanya  08.06.2019 23:50
Набор солдатиков со скидкой 10% стоит 720 рублей. какова его цена без скидки?...
Прлплмопо Прлплмопо  08.06.2019 23:50
На книжной полке стоит собрание сочинений в 30 томах.сколькими различными их можно переставить, что бы тома 1 и 2 стояли рядом?...
валерияС1 валерияС1  08.06.2019 23:50
Вдвух сундуках лежат 6 карт за карты из первого сундука заплатили 12 лир а за карты из другого 24 лиры сколько карт лежат в каждом сундуке если они имеют одинаковою цену. по действиям...
cleverprincess cleverprincess  08.06.2019 23:50
Втреугольнике со сторонами 6 и 2 проведены высоты к этим сторонам. высота, проведенная к первой стороне равна 1, найди вторую высоту...
Irina1440 Irina1440  08.06.2019 23:50
Із двох сіл відстань між якими 7,6 км одночасно назустріч один одному вийшли два пішоходи. швидкість одного пішохода 4,6 км/год, а іншого - 4,9 км/год. через скільки хвилин пішоходи...
karpovkonstanti karpovkonstanti  08.06.2019 23:50
Найдите значение выражения (6b-9)(9b+6)-9b(6b+9) при b=5,3...

Популярные вопросы