Докажите тождество (см. вложение)
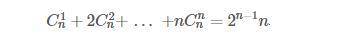
Другие вопросы по теме Математика
Популярные вопросы
- География Нужно написать тектонические структуры, форма рельефа,...
1 - решить задания 6.1 и Завтра сдавать...
2 - 4. Мәтінге сүйеніп, аспалы бақтың алғашқы нұсқасын сипатта. Жалпы...
1 - Как читать климатограммы (можно подробно...
3 - Завдання № 1.Встановити відповідність (виконати у зошиті) 1) Безособове...
2 - ответьте на вопросы: 1. Кто ввел термин «Великий Шёлковый путь»?...
1 - бан за ерунду Соотнеси название термина с его определением и заполни...
2 - Помагите решить информатика 9 класс Тест по теме «Программное...
2 - Охарактеризовать лирического героя стихотворения Тургентева Голуби...
2 - Реферат о Центрально - Чернозёмном районе ...
3
Рассмотрим слагаемое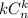 ,
, 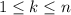 .
.
Это количество сочетаний из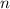 элементов по
элементов по 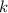 , повторенное столько же раз.
, повторенное столько же раз.
Выстроим одну из комбинаций из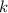 элементов в строчку. Домножив на
элементов в строчку. Домножив на 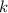 , получим квадрат
, получим квадрат  элементов. То есть
элементов. То есть 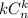 — это множество квадратов. Теперь построим квадратную таблицу
— это множество квадратов. Теперь построим квадратную таблицу 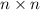 (см.рис)
(см.рис)
В первой строке будут первые строчки большинства квадратов, кроме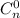 . Во второй строчке уже не будет
. Во второй строчке уже не будет 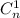 , поскольку квадраты
, поскольку квадраты 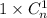 целиком умещаются в первой строчке. И т.д. Причем будет отсутствовать вычитаемое
целиком умещаются в первой строчке. И т.д. Причем будет отсутствовать вычитаемое 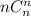 , т.к. этот квадрат содержит все строчки.
, т.к. этот квадрат содержит все строчки.
Пусть искомая сумма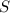 . Сложив все строчки, получим
. Сложив все строчки, получим 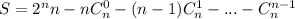 , поскольку
, поскольку 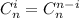 , перепишем сумму:
, перепишем сумму:
Пошаговое объяснение:в приложении