1. Математика
  2. Докажите по индукции данное

Докажите по индукции данное утверждение по подробнее


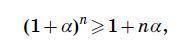
Докажите по индукции данное утверждение по подробнее

Maria2009 Maria2009    3   11.10.2020 05:38    0

Ответы
pula04 pula04  11.10.2020 06:01

Условие не является полным. Это известное неравенство так называемое неравенство Бернулли и оно гласит, что для \alpha \geq -1 имеет место неравенство 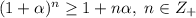(1+\alpha)^n\geq 1+n\alpha,~ n \in Z_+

1) При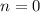 n=0 база индукции выполнено: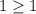 1\geq 1

2) Предположим, что для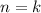 n=k имеет место неравенство

(1+\alpha)^k\geq 1+k\alpha

3) Докажем, что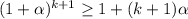 (1+\alpha)^{k+1}\geq 1+(k+1)\alpha

(1+\alpha)^{k+1}=(1+\alpha)(1+\alpha)^k\geq (1+k\alpha)(1+\alpha)= 1+k\alpha+\alpha+k\alpha^2\geq\\ \\ \geq1+k\alpha+\alpha=1+(k+1)\alpha

Неравенство верно из предположения 2). Утверждение доказано.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
ARTEMONUM ARTEMONUM  24.05.2019 23:00
Уелдоса есть курицы и козы. козы меньше куриц в 3 раза. у куриц и коз общее 40 ножек. сколько у елдоса куриц и коз? с решением...
mrvipdanchannep0793v mrvipdanchannep0793v  24.05.2019 23:00
Турист направлялся из одного города в другой.он приехал 2 ч. на автомобиле со скоростью 70км.ч, потом 4 ч. шёл пешком со скоростью 5км.ч,и после этого ему осталось пройти 14 км....
костя665 костя665  24.05.2019 23:00
Выполните вычисления 9дм8см-2дм4см*4=...
tsartsar tsartsar  24.05.2019 22:50
Сочинение на тему роль танцев в моей жизни...
Dimaplayfifa1611 Dimaplayfifa1611  24.05.2019 22:50
, он ответил: «если отсчитать подряд 9 чисел, начиная с 2 через одно число, последнее число разделить на 3 и прибавить 2. то вы узнаетесколько мне лет». *скольковаселет?...
Felipinec Felipinec  24.05.2019 22:50
1.на карте казахстана рядом с впадиной карагие написано число-132м, рядом с возвышенностью тарбагатай написано 2930м. что обозначают эти числа?...
neznakomka1408 neznakomka1408  24.05.2019 22:50
Асхат купил марку за 50 тг краски за 120 тг и лотерейный билет за 100 тг он продал марку за 70 тг, краски за 100 тг и лотерейный билет за 130 тг. сколько прибыли получил асхат...
Katyaguccigang Katyaguccigang  24.05.2019 22:50
Римские цифры имеют следующий вид: i — один, l — пятьдесят, v — пять, с — сто, x — десять, d — пятьсот, м — тысяча. запиши арабскими цифрами числа: mdl, mdcx, mdcxv, mdcciv....
kuekkukov kuekkukov  24.05.2019 22:50
Вкорзину с грибами добавили 7 грибов. сколько грибов надо взять из корзины, чтобы в ней стало на 10 грибов меньше, чем было сначала?...
vladdancer vladdancer  24.05.2019 22:50
Найти сторону квадрата,если его периметр равен 0,032 м...

Популярные вопросы