Докажите что треугольник и равны

​

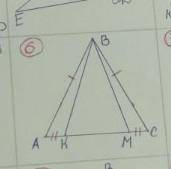
Дано:△ABC; AB = BC;

K, M ∈ AC; AK = MC

Доказать: △ABM = △KBC

Доказательство:

△ABC - равнобедренный => ∠A = ∠C;

AB = BC;

AK = MC, KM - общая => AM = KC = AK + KM

=> △ABM = △KBC (по I признаку равенства△)

ч.т.д.

ΔАВС - равнобедренный (АВ=ВС)

Теорема: в р/б треугольнике углы при основании равны.

Следствие: ∠ВАС=∠ВСА.

Вывод: в ΔВАК и ΔВСМ равны две стороны (АВ=ВС, АК=СМ) и угол между ними.

Следствие: ΔВАК=ΔВСМ по первому признаку (две стороны и угол между ними).