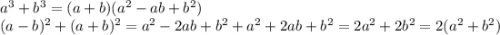Докажите что сумму кубов пяти последовательных натуральных чисел можно разложить в произведение трех целых чисел каждое из которых больше 1
Другие вопросы по теме Математика
Популярные вопросы
- Выбери (копируй) правильный ответ из списка: (ctrl+b, ctrl+i, ctrl+u,...
1 - Скласти рівняння перетворень назвати продукти реакції. метан – етин...
1 - 2mg(100л)+o2=2mgo+120кдж(xкдж) найдите массовую долю ! ...
3 - Медианы треугольника abc пересекаются в точке m. а) докажите, что треугольники...
2 - Сурок через 15минут нужно построить аккорды от ноты си м6, ув53 , и...
3 - Кут aob дорівнює 135°.через точки a і b проведено прямі, які паралельні...
3 - Для определения объема камня неправильной формы его перевязали нитью...
3 - Вкакой из солей формулы которых даны ниже металл x трех валентен...
2 - Узнай, будут ли прямые 4x+5y−7=0 и 8x−3y−1=0 пересекаться в точке a(0,5;...
2 - Язык. назовите авторов сказок про кошку шарлотту. таких сказок несколько...
1
Ч.т.д.
Формулы: