Популярные вопросы
- Впишите слова –: do, does, did, will 1.… you visit your granny next...
2 - Решите уравнение (5^x-2)+(2^x+1)+(2^x+) = 0....
2 - Составте предложения на казахском : тамақты əэірлеу , анаға көмектесу...
1 - It has got a big head and а small bоby...
2 - Продолжите: 1)в слове государственный пишется -нн-, потому не в слове...
2 - Решите ! ! тест по временам past simple, continuous, pastperfect or...
1 - Проверяемые безударне гласные в корне слова хорошо в лесу в полдень.зеленые...
3 - Какое строение кометы? из чего состоит ее ядро?...
1 - Слово экипаж имеет несколько значений придумайте и запишите предложение...
3 - Начертите окружность, диаметр которой равен 6 см. проведите радиус...
2
Докажем это методом математической индукции.
1. Пусть n=1:
2. Пусть n=k. Предположим, что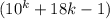 кратно 27.
кратно 27.
3. Пусть n=k+1. Докажем, что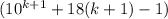 кратно 27.
кратно 27.
Первое слагаемое делится на 27, потому что, во-первых, есть сомножитель 9, а, во-вторых, скобка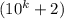 представляет собой число вида
представляет собой число вида  , которое делится на 3 по признаку делимости, значит все слагаемое делится на 3·9=27. Второе слагаемое делится на 27 по предположению, сделанному на втором шаге. Значит и вся сумма делится на 27.
, которое делится на 3 по признаку делимости, значит все слагаемое делится на 3·9=27. Второе слагаемое делится на 27 по предположению, сделанному на втором шаге. Значит и вся сумма делится на 27.