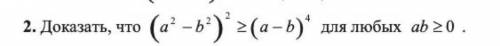
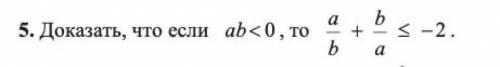
Другие вопросы по теме Математика
GamerPro3922
30.09.2019 02:50
ykropmen
30.09.2019 02:50
TheTanyaStar2k
30.09.2019 02:50
GeorgeWashUSA
30.09.2019 02:50
nasty1512200229
30.09.2019 02:50
spydemise
30.09.2019 02:50
Популярные вопросы
- Свидригайлова есть что-то, что их объединяет, поэтому Свидригайлов...
1 - Ағаттың азабы бөлімі бойынша жоспар құра қойыңыздарӨте керек болып...
3 - Линейное неравенство с одной переменной. Решение линейных неравенств...
3 - Составьте синквейн на тему «Вода – источник жизни» Если вы это не...
1 - Что такое солнечные консервы...
1 - «Тәуелсіздік» тақырыбына синквейн (бес жолды тақпақ) дайында.Бес...
3 - Взято по одному молю гелия неона и аргона при одинаковой температуре...
3 - тапсырма. Мына етістіктерге ауыспалы осы шақтың жұрнағын қосыңыз...
1 - Площадь треугольника. Урок 1 Найди площадь треугольника.ответ: кв....
3 - Что относится к устройствам передачи информации? *...
1
(a-b)^4 = ((a-b)^2)^2)
(a-b)^2 = aa + bb - 2ab
(aa - bb)^2 ^ (aa + bb - 2ab)^2
берем корень:
aa - bb ^ aa + bb - 2ab
aa ^ aa + 2bb - 2ab
2ab ^ aa + 2bb
ab ^ aa/2 + bb
aa ^ 2 + bb >= 0
a, b >= 0 => (a^2-b^2)^2 >= (a-b)^4