Доказать сходимость ряда и найти его сумму от бесконечности до n=1 1/n^2+5n+4

Ответы

SHERBINADARYA00 10.10.2020 17:09

ответ: 13/36

Пошаговое объяснение:

$an = \frac{1}{n^{2}+5n+4} = O(\frac{1}{n^{2} })$

А так как данный ряд сходится, то сходится и исходный по признаку сравнения.

Чтобы найти сумму ряда, нужно разложить дробь на простейшие.

an =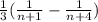 $\frac{1}{3}(\frac{1}{n+1} - \frac{1}{n+4})$

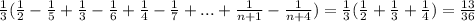Sn = $\frac{1}{3}(\frac{1}{2} - \frac{1}{5} + \frac{1}{3} - \frac{1}{6} + \frac{1}{4} - \frac{1}{7} +... + \frac{1}{n+1} - \frac{1}{n+4} ) = \frac{1}{3}(\frac{1}{2} + \frac{1}{3} + \frac{1}{4}) = \frac{13}{36}$ , n ⇒ ∞

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

Evelina0889 27.07.2019 04:20

Магазин продал за день 32кгвиш варенья и 40кг варенья мал малинового на 4 банки больше сколько всего продали...

vddrobysheva 27.07.2019 04:20

Одна шестая часть отрезка 12см чему равна длина отрезка...

ange4 27.07.2019 04:20

Решить , . площадь этажа составляет 240 квадратных метров. чему равна площадь этого этажа на плане с масштабом 1: 1000?...

logan9 27.07.2019 04:20

Запишите в виде процентов десятичные дроби 6,51; 2,3; 0,095...

7777kby777777777778 27.07.2019 04:20

Прямоугольный участок, ширина которого 60 м, а длина на 30 м больше, обнесён забором из металлической сетки высотой 1.6 м. найдите площадь металлической сетки....

PRO11116 27.07.2019 04:20

Решить по за 3 класс. вычисли периметр прямоугольника,если его площадь равна 140 см.кв. заранее всем . с меня 30бб...

evasaidova91 27.07.2019 04:20

Найди среднее арифметическое чисел 32.4; 41; 27.95; 46.9; 55.75;...

kata198722 27.07.2019 04:20

Из города в противоположных направлениях выехали грузовик и мопед скорость грузовика 47 км в час обеда 33 километров час какое расстояние по шоссе и будет между ними...

TomaSharik 27.07.2019 04:20

Сторона клумбы квадратной формы равна 8 м. 1/16 всей площади клумбы засажена нарциссами а остольная площадь тюльпанами. на какой площади клумбы посажены тюльпаны?...

jyljokgorsheni1 27.07.2019 04:20

Колесо имеет 5 спиц углы между соседними спицами равны найдите величину угла в градусах который образуют две соседние спицы...

Доказать сходимость ряда и найти его сумму от бесконечности до n=1 1/n^2+5n+4

Популярные вопросы