Доказать равенство с определения предела функции (по Коши или по Гейна)
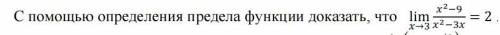
Другие вопросы по теме Математика
Популярные вопросы
- Сократите дробь корень из 5 +5 в знаменателе 4 корня из 5...
1 - Знайдіть довжину медіани ам трикутника авс, якщо а(7; -2), в(-5;...
1 - В5 классе 30 учащихся. на каникулы им дали придумать для олимпиады...
1 - Решите уравнение 19x-21y=2 в целых числах.(слабо! )...
1 - Знайти у, якщо відстань між точками а і в дорівнює 5, а(-1; у)...
1 - Сравните власть императоров цинской династии с властью кого- либо...
1 - На встречное движение. одна птица летела со скоростью 8км/мин ,а...
1 - По муму : почему тургенев решил так закончить о муму?...
3 - Lim x стремится к 0 3x^3+x^2/x^5+3x^2-2x^2...
1 - Знайти точки перетину прямих , рівняннями 6х - 14у - 6 = 0 і 2х...
1
Пошаговое объяснение:
Пусть ε - сколь угодно малое положительное число. Мы докажем утверждение, если найдём такое число δ>0, если для всех x∈(3-δ; 3+δ) будет выполняться неравенство /(x²-9)/(x²+3*x)-2/<ε. Это неравенство равносильно двойному неравенству 2-ε<(x²-9)/(x²+3*x)<2+ε. Их общим решением является x∈(3/[1+ε];3)∪(3;3/[1-ε]). Так как число 3/(1+ε) "ближе" к 3, чем число 3/(1-ε), то возьмём δ=3-3/(1+ε)=3*ε/(1+ε). Таким образом, число δ найдено, а это и доказывает справедливость равенства.