Доказать равенство для невырожденной матрицы А произвольного порядка
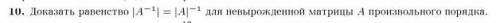
Другие вопросы по теме Математика
Популярные вопросы
- Где произрастатают дикорастущие растения?...
2 - Составьте 6 примеров на ек и на ик надо...
3 - Сторона ав ромба авсд равна а, один из углов равен 60гр. через сторону...
1 - Выписать сравнения эпитеты предложения относящиеся к татьяне из рассказа...
1 - Перевести на современный язык подал царю челобитную за своей рукой...
2 - Какой автор написал стих о крестьянских детях...
1 - Обедини слова близкие по смыслу и запиши их групами: отведать,наброситься,почувствовать,налететь,папробывать,испытать...
1 - Что является наименьшим адресуемым элементом оперативной памяти...
3 - Как изменится период колебания маятника, если переместить его с земли...
2 - Составить словосочетания со словами ароматное, автомобильный, лучистый(...
3
1. Транспонирование (обозначается знаком T): транспонированная матрица получается из исходной матрицы путем замены строк на столбцы.
2. Умножение матриц (обозначается знаком *): результатом умножения матрицы А на матрицу В является матрица С, где каждый элемент с индексами [i, j] определяется как сумма произведений элементов i-й строки матрицы А на j-й столбец матрицы В.
3. Обратная матрица: для невырожденной матрицы А существует обратная матрица A^(-1), такая что A * A^(-1) = A^(-1) * A = E, где E - единичная матрица.
Теперь приступим к доказательству равенства.
Данное равенство можно переписать в виде:
(A * A^(-1))^T = (A^(-1))^T * A^T.
Так как мы знаем, что A * A^(-1) = A^(-1) * A = E, то:
(A * A^(-1))^T = E^T = E.
Также, обратная матрица симметрична относительно транспонирования, то есть:
(A^(-1))^T = (A^T)^(-1).
Таким образом, мы получаем:
(A * A^(-1))^T = (A^(-1))^T * A^T = (A^T)^(-1) * A^T.
Из полученного равенства следует, что:
(A * A^(-1))^T = (A^T)^(-1) * A^T = E.
Таким образом, мы доказали равенство для невырожденной матрицы А произвольного порядка.