Доказать равенства, пользуясь соответствующим определением предела (ничего не понял из этой темы, поэтому требуется желательно расписать подробно)

Другие вопросы по теме Математика
Популярные вопросы
- Выписать сначало слова которые пишутся по произношению, затем...
1 - Собака несчастная опасна. ведь ей не везет в этой жизни ужасно....
3 - Концентрация ионов водорода в растворе равна 0,00046 моль/г вычеслить...
1 - Write six sentencens about your classroom с переводом...
2 - Из пункта a в пункт b расстояние между которыми 54 км выехал...
2 - Вычислете дленну ломаной mnkpef, если mn=42мм,nk=38мм,kp=19мм,pe=12мм,ef=29мм....
3 - Вчем состоит сложность изучения первобытного общества?...
3 - Впачке 120 тетрадей . тетради в клетку составляют 3/5 этой пачки....
3 - Нужно сделать блок-схему! определить суммарный объем в литрах...
1 - Определите массу кислорода и объем углекислого газа, которые...
1
Пошаговое объяснение:
По определению: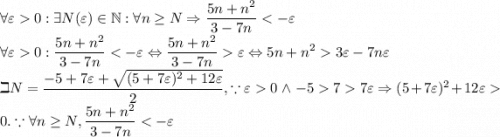
ЧТД
По определению:
ЧТД