Доказать по определению предела функции, что
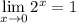
Другие вопросы по теме Математика
Популярные вопросы
- Запиши глаголы в времени заранее...
1 - Промышленность,где используют различные вещества растительных клеток...
2 - Inot having breakfast now they not going to school by bus nick not doing lus...
2 - Найти значение выражения , если значение х удовлетворяет условию = 1-х...
3 - Как образуются артезианские источники?...
3 - Какие при не обратимых реакциях: 1. при сжигании спички и газа 2. при варки...
2 - Маятник массой 200г имеет длину 2м. отклонили от положения равновесия на 6см....
1 - Написать программу вычисления площади кольца используя процелуру вычисления...
3 - Куб, поверхность которого окрашена, распилили на 27 одинаковых по размеру кубиков.сколько...
3 - За 4 мин тело осуществило 700 колебаний. какой путь тело за это время если...
3
Пошаговое объяснение:
Вспомним определение предела
Для нас
Тогда
Получим, что
А это верно по определению (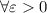 ) и из-за малости х (функция монотонно возрастает)
) и из-за малости х (функция монотонно возрастает)