1. Математика
  2. Доказать, что заданная функция

Доказать, что заданная функция z=f(x,y) удовлетворяет данному уравнению

nnn0212 nnn0212    2   25.08.2019 02:10    2

Ответы
гуля429 гуля429  09.09.2020 01:55
Докажем так: найдем частные производные функции по x и y
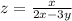
z= \frac{x}{2x-3y}
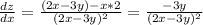
\frac{dz}{dx} = \frac{(2x-3y)-x*2}{(2x-3y)^2} = \frac{-3y}{(2x-3y)^2}
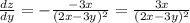
\frac{dz}{dy} = -\frac{-3x}{(2x-3y)^2} = \frac{3x}{(2x-3y)^2}

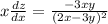
x\frac{dz}{dx} =\frac{-3xy}{(2x-3y)^2}
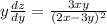
y\frac{dz}{dy}=\frac{3xy}{(2x-3y)^2}

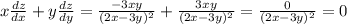
x\frac{dz}{dx}+y\frac{dz}{dy}=\frac{-3xy}{(2x-3y)^2}+\frac{3xy}{(2x-3y)^2}=\frac{0}{(2x-3y)^2}=0
ПОКАЗАТЬ ОТВЕТЫ
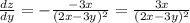
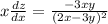
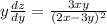
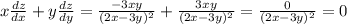
Другие вопросы по теме Математика
pykanchik pykanchik  08.12.2019 21:27
Построить кривые второго порядка (окружность, эллипс, параболу) по заданным уравнениям (...
DimaLim DimaLim  08.12.2019 21:28
Чому дорівнює різниця між добутком і сумою ненульових цифр числа 2 у 10 степені у десятковому записі?...
petyasmolin petyasmolin  08.12.2019 21:29
Жуков, замухамбиев, мосарев, коноводов. в каждой фамилии имеется одно слово, объединяющее общей темой все фамилии. что это за тема❓​...
Ked4 Ked4  08.12.2019 21:29
Решить у 2 кг сплаву олова,цинку и меди е 800 г олова и цинку 400 г.скильки мистыться цинку и миди у 3 кг такого самого сплаву? ​...
baburinyaroslav baburinyaroslav  08.12.2019 21:31
Углы треугольника abc равны 15,8° и 44°53 найдите третий угол...
natalalebedvt71 natalalebedvt71  08.12.2019 21:32
Валентин подарил виктории розы и орхидеи, причём орхидей было в 4 раза меньше, чем роз. сколько роз подарил валентин, если известно, что их было на 51 больше, чем орхидей? с условием,...
nadijagordijenp07vwr nadijagordijenp07vwr  08.12.2019 21:33
Число а становить 40 від числа b скільки відсотків число b составляет от числа а...
tagirrulit tagirrulit  08.12.2019 19:42
На растояние 8 см от центра окружности проведена хорда длиной 30 см . вычислите радиус окружности...
AkiraK666 AkiraK666  08.12.2019 19:42
Выражение (-a)*(-b)*(-c)*(-d) -0,8*(-3x)*5y*(-4) -1/3a*(-3/4b)*(-4/5c)...
Мессалина1 Мессалина1  08.12.2019 19:43
Списал и ничего не понимаю ( нужно было ли в этом примере рисовать рисунок, чтобы найти ответ или и еще вопрос, куда делась вомьмёрка? почему её ни применили в решении? или применили,...

Популярные вопросы