Доказать,что треугольник авс подобен треугольнику MNK,если угла А=М угл В=углу N ВС=4 АС=5 NK=6 и найти длину мк
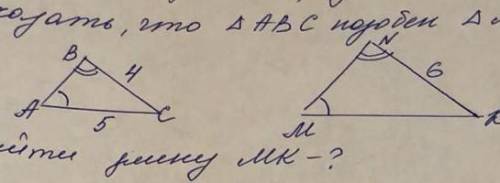
Другие вопросы по теме Математика
Популярные вопросы
- 3. каждый из 36 учеников класса изучают хотя бы один иностранный язык...
3 - Решите систему уравнений: , , 2(3х + 2у) + 9 = 4х +21; 2х + 10 = 3 –...
2 - Необычная для меня с подпрыгивающей пружиной, решить пружина массой...
2 - Решите неравенство: 125*5^(2*x-1) 1/25 желательно подробно....
3 - 6-х/3=х/7 решить уравнение напишите подробно как вы делали ответ должен...
3 - Как это решается? к 140 г 15 % ного раствора сахара долили 160 мл воды.каково...
1 - Сравните ливонскую и северную войну. выберите и запишите в первую колонку...
3 - 4. фирма “прогресс” заключила договор аренды с петровой, согласно которому...
2 - Было отремонтировано от всех станков цеха. сколько станков в цехе, если...
2 - 3. запишите все трехзначные числа, состоящие из следующих цифр (цифры...
2
Из условия задачи получаем следующую информацию:
- Угол А равен углу М
- Угол В равен углу N
- Сторона ВС равна 4
- Сторона АС равна 5
- Сторона NK равна 6
Теперь мы можем приступить к решению.
1. Сначала докажем, что углы АВС и МNK равны друг другу:
Угол А равен углу М (из условия)
Угол В равен углу N (из условия)
Таким образом, углы АВС и МNK равны друг другу.
2. Затем докажем, что стороны АВС и МNK пропорциональны:
Рассмотрим отношение длин сторон. В треугольнике АВС, сторона ВС равна 4, а сторона АС равна 5. В треугольнике МNK сторона NK равна 6.
Отношение сторон ВС и NK равно: 4/6 = 2/3
Отношение сторон АС и МК равно: 5/КМ (пусть КМ обозначает длину стороны МК)
Из пропорции 2/3 = 5/КМ мы можем решить уравнение на КМ:
2КМ = 3 * 5
2КМ = 15
КМ = 15/2
КМ = 7.5
Итак, мы доказали, что треугольник АВС подобен треугольнику МNK, так как соответствующие углы равны, и соответствующие стороны пропорциональны. Длина стороны МК равна 7.5.