Доказать, что существует бесконечно много таких натуральных чисел N, что число 4N^2+1 делится и на 5, и на 13
Другие вопросы по теме Математика
Популярные вопросы
- Көмектесінізші, осы есепті шыгар алмай жатырмын я не могу опубликовать...
2 - Литература. вопрос номер 4...
2 - начертите в тетради ломаную Изображëнную на рисунке 20 измерьте длины...
3 - 7 клас вправа 18 заболотний...
1 - Упрочтить вирвжение (5х_3у)(5х+3у)+(3х_5у)(3х+5у)=...
3 - Прочти текст и выдели оранжевым цветом слова, подтверждающие, что А.С....
3 - 5 кг разложили в банки по 500 г и в банки по 200г банок по 500 г оказалось...
1 - Составьте по каждому словосочетанию предложение. make your bed, make...
2 - Найдите значение выражения 1,3+1,1...
1 - Для элемента с электронной конфигурацией 1s2 2s2 2p4 впишите в таблицу...
1
Пусть , тогда
, тогда 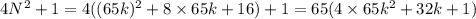 , то есть
, то есть 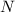 делится на 65, а значит, на 5 и на 13 одновременно.
делится на 65, а значит, на 5 и на 13 одновременно.
Итак, для любого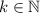 возьмем
возьмем  и получим, что
и получим, что  делится и на 5, и на 13
делится и на 5, и на 13
Выберем N=65к+4, где к любое натуральное
Пошаговое объяснение:
чтобы число делилось на 5 надо, чтобы 2N заканчивалось на цифру 8 или 2, т.е. 2N=10m+8. тогда 4N^2+1=100m^2+160m+65
или 2N=10m+2 ,
Рассмотрим первый случай.
Нужно, чтобы 91*m^2+9m^2+156m+4m+65 делилось на 13.
Для этого
Нужно, чтобы 9m^2+4m делилось на 13.
или, то же самое, что
m*(9m+4) делилось на 13.
Выберем m=13*к
Итак достаточно взять любое 2N=130к+8, где к любое натуральное.
N=65к+4