Доказать, что при любом n принадлежащем множеству Натуральных чисел равенство верно.
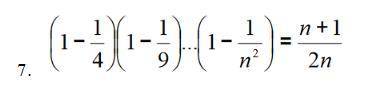
Другие вопросы по теме Математика
Популярные вопросы
- Плот плывёт со скоростью 8 м/мин.Сколько метром проплывёт плот за 5...
3 - Найди неизвестный угол среди треугольников...
3 - Составьте уравнение окружности с центром С и радиусом R, если С(4;...
1 - 1. что такое доля 2. что такое дробь 3. из чего состоит дробь 4. что...
1 - Поезд идёт со скоростью 684 км/ч. Сколько метров он проезжает за одну...
1 - До ть написати лист до говорющої риби із твору Емми Андієвської «Говорюща...
3 - Рассмотрев особенности семейных растений Укажите В чём их отличие от...
1 - Начертить в масштабе 1:1 деталь А, ввернутой в деталь Б. Нанести габаритные...
2 - Хто бувкріпаком у ХлестаковаА) ІванБ) СтепанВ) ПетроГ) Осип...
1 - Дмитро виготовляє на уроці праці брусок, об єм якого має бути 0,06...
1
Думаю, автор задания хотел сказать при любом n>1. Будем исходить из этого предположения. При n=2 имеем
В самом деле,
Утверждение доказано с математической индукции.