1. Математика
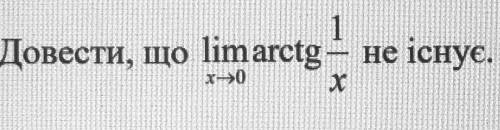
  2. Доказать что лимит не иснует

Доказать что лимит не иснует


Доказать что лимит не иснует

лукашук лукашук    3   05.12.2020 00:49    0

Ответы
darinanugmanova darinanugmanova  12.02.2021 19:32

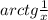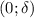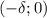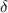Функция arctg\frac{1}{x} определена в (0; \delta) и (-\delta; 0) для сколь угодно малых \delta.

Тогда воспользуемся теоремой о связи двустороннего предела с односторонними: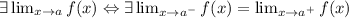 \exists\lim_{x \to a} f(x) \Leftrightarrow \exists\lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x).

\lim_{x \to 0^-} arctg\frac{1}{x}=-\frac{\pi}{2}.

\lim_{x \to 0^+} arctg\frac{1}{x}=\frac{\pi}{2}.

Односторонние пределы не равны, следовательно двустороннего не существует. Что и требовалось доказать.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
llboyn llboyn  22.05.2020 18:22
Обчислити площу бічної поверхні правильної трикутної призми,сторона якої дорівнює 20см, а висота - 9см...
Hicoleta Hicoleta  22.05.2020 18:22
У=5 в степени -х Яку властивість із наведених має функція...
Ddaannjjdb Ddaannjjdb  23.05.2020 17:30
Задана арифметическая прогрессия. первый член равен 12, разница прогрессии равна 2. Найти сумму пятидесяти одного члена заданной прогрессии * а 3468 б 612 в 3213 г 3162...
artem28 artem28  22.05.2020 18:21
3.Найти производные следующих функций: а) 2/χ^3 ─ 3χ^2 = б) 3√(χ^3 ) ─ 7χ^6 = в) (3 ─ χ) (6 ─ ∛(χ^(7 ) )─ χ)^3 = г) χ^3/(5 ─ √(χ^3 ))...
ДанилкаМаксимка ДанилкаМаксимка  22.05.2020 18:21
умоляю Нужно найти числа, за этими двумя формулами: Числа: 5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20. Формулы: 1. x #(не равно) 3k - 2 2. x #(не равно) 4k + 3...
habman habman  22.05.2020 18:21
НАЙДИТЕ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ :::...
kotikmotik55 kotikmotik55  27.06.2019 06:40
Переведите ! 8 час 11 мин = сек 1 км 52 метра = 1 тонна 2 центнеров 73 кг = 28 часов 53 мин = . заранее !...
iwanttobelllllive iwanttobelllllive  27.06.2019 06:40
Гриша с дедушкой пошли в тир. уговор был такой: гриша делает 5 выстрелов и за каждое попадание в цель получает право сделать ещё 2 выстрела. всего гриша сделал 13 выстрелов. сколько...
dylanboy dylanboy  27.06.2019 06:40
Вычислите площадь круга, радиус которого 3 см. (п=3)....
Darya0012 Darya0012  27.06.2019 06:40
Решите по действиям (22796-6377)*45+44449-38040/30 17*(17598*8/42*12-275-412)...

Популярные вопросы