Доказать, что функция и g(x) при x→0 являются бесконечно малыми одного порядка малости.
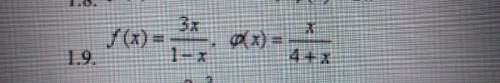
Другие вопросы по теме Математика
Популярные вопросы
- это все решить Алгебра все отдаю...
3 - До якої відміни належить слово мрія...
3 - Ветровое колесо радиусом 1,2 м имеет период обращения 1,5 с....
1 - Привіт. Хто робив Контрольну з біології 7 клас Л.Остапченко параграф...
1 - 1. Які трагічні картини побачив Шевченко, коли повернувся в Україну?...
1 - подготовить ответ к зачету на вопрос Логическое сложение. Таблица...
1 - Чого повчає Р. Стівенсон у романі «Острів скарбів»...
3 - Скажите ответ нужно Сколько целых чисел принадлежит промежутку:...
3 - Для чого призначені пристрої, що входять до складу мультимедіного...
2 - 30. Выберите вариант, в котором числительное, стоящее перед существительным,...
1
Доказательство:
Функции будут бесконечно малыми одного порядка малости, если предел их отношения при x→0 будет конечным.
Таким образом, функции являются бесконечно малыми одного порядка малости