Доказать, что для всех натуральных n верно неравенство:
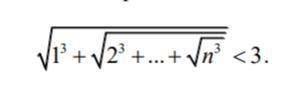
Популярные вопросы
- Можете подсказать, 11 класс. Если в первом полугодии стоит 4, а во втором полугодии...
1 - Рівняння реакції сполучення - горіння простої речовини...
3 - Вася в магазине купил товары на 1200 рублей. На покупку мыши он потратил 30%...
2 - Обчисліть:125 ( 26) 1(-2)-2313...
3 - ів! Рівняння руху тіла х=10-3t+2t2.яку швидкість буде мати тіло через 5 сек...
1 - Що позначає вираз Шануйся на другий раз...
3 - 3-тапсырма. Берілген сөйлемдерге синтаксистік талдау жаса. 1. Біз тәуелсіз, егеменді...
3 - 4.It’s taking a long time to build new power lines because the construction company…….....
2 - 2 4. У покупателя 500 рублей. Он потратил- Сколько рублей потратил покупатель?...
3 - Определить число и лицо на слово время...
3
Пусть последовательность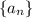 такова, что для всех
такова, что для всех  выполнено неравенство
выполнено неравенство 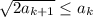 . Тогда верно неравенство
. Тогда верно неравенство 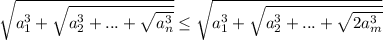 . Это легко видеть, заменяя члены с использованием неравенства.
. Это легко видеть, заменяя члены с использованием неравенства.
В нашем случае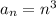 , неравенство
, неравенство 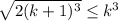 верно для всех натуральных
верно для всех натуральных 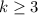 . Значит, искомая сумма не превосходит
. Значит, искомая сумма не превосходит 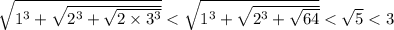 . Для
. Для 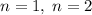 очевидно.
очевидно.