Доказать что (6^2n-1 +1) делится на 7
Другие вопросы по теме Математика
Популярные вопросы
- Найдите наименьшее целое значение неравенства...
2 - зимой задние колеса некоторых грузовиков туго обвязывают масивными цепями...
1 - . Чому Мольєр у фіналі п єси не розкриває маркiзi Дорімені того, що Доран...
2 - Найди значения выражения 85*а, если А = 100;а=12....
1 - Твір-оповідання за картиною, опираючись на поданий початок (10-12) речень...
2 - В течение 0,5 ч пешеход двигался со скоростью 4 км/ч, а следующий 1 ч...
1 - Решите уравнение 2 +7x — 4х = 0....
1 - Список комплементов для обслуживающего персонала...
3 - Выполни 2.Используя текст учебника (параграф 28 стр 110-111)Заполни...
3 - Скласти 1 речення з відокремленою обставиною, вираженою прийменником...
2
Применим здесь метод математической индукции.
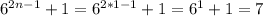
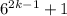 кратно 7
кратно 7
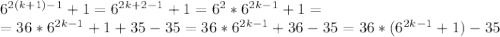
1) При n=1 имеем:
7 делится на 7
2) Предположим, что для некоторого k число
Докажем, что это число будет кратно 7 для k+1:
Выражение в скобках делится на 7 согласно нашему предположению, и умноженное на 36, оно всё равно делится на 7 :)
Число -35 также делится на 7.
Значит и их сумма тоже делится на 7, что и требовалось доказать...