Доказать, что 3³⁽ⁿ⁺¹⁾ - 2³⁽ⁿ⁺¹⁾ кратно 19
Другие вопросы по теме Математика
Популярные вопросы
- 1) понизили на 30% а потом повысили на 30% ответ- 2) повысили на...
3 - Виписати країни світу які займають лідируючі позиції за кожним видом...
1 - . Найти все целые значения k, при которых корнем уравнения |k|х=6х‒24...
1 - Перепишите ток не в тетрадь ...
2 - Основные классы неорганических веществ >...
2 - решить З точок М і N, які лежать відповідно у двох перпендикулярних...
1 - Касым хан и Хакназар хан 1.в период првления хана Касыма Казахское...
2 - 2.Найдите во вступительной статье информацию, содержащую размышле-...
2 - выбор человеком наиболее ценных в хозяйственном или декоративном...
1 - ВИДЫ ДАТЧИКОВ ПРИМЕРЫ ПРИМЕНЕНИЯ (3 примера) Датчик температуры...
2
Пошаговое объяснение:
Докажем гипотезу с метода математической индукции.
1. База индукции при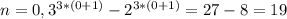 кратно 19
кратно 19
2. Шаг индукции. Предположим, что при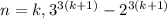 кратно 19. Докажем, что при при
кратно 19. Докажем, что при при  также будет кратно 19.
также будет кратно 19.
Уменьшаемое делится на 19, т.к.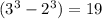 , а вычитаемое делится на 19, т.к. по предположению индукции
, а вычитаемое делится на 19, т.к. по предположению индукции  делится на 19.
делится на 19.
Следовательно и разность делится на 19.