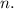Доказать, что (17^n-1) делится нацело на 16 для любого натурального числа n. Подскажите
Другие вопросы по теме Математика
Популярные вопросы
- Определи при паразитических плоских червей к паразитическому образу жизни...
3 - Унаслідок збільшення тиску в 1,5 раза об єм газу зменшився на 30 мл. Визначте...
1 - с английским. В первом задании только 1 и 4 предложения надо сделать. А в...
3 - Какие налоги были в Золотой орде?...
2 - Вырази в миллиджоулях. 5,9⋅ 10 −4 Дж=0,00059Дж=мДж...
3 - Что находится в выданной пробирке (слабый электролит или неэлектролит), если:её...
2 - Найдите длину вектора -2а+3в если а(2;-1;3) , в(-1;2;5) ...
2 - Синтаксический разбор. В воздух.. закружилась сухая тр..ва л..ства сорва(н/нн)ая...
1 - А можете с ответами? Ex.7. Answer the questions on the text: 1. What does...
3 - 16. Шлюб подружжя Броньків було розірвано у міському суді. Розглядаючи спір...
3
Докажем методом математической индукции.
1) При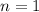 выполнено
выполнено  .
.
2) Предположим, что при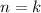 выражение
выражение 
3) Докажем теперь при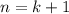
Первая скобка делится на 16 по предположению 2), а слагаемое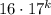 очевидно делится на 16, следовательно и сумма этих слагаемых делится на 16. Следовательно, выражение
очевидно делится на 16, следовательно и сумма этих слагаемых делится на 16. Следовательно, выражение 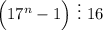 для любых натуральных
для любых натуральных