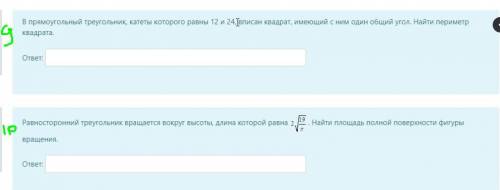
Добрый день решить два задания надо.

1.

В Δ АВС  вписан квадрат СМKP

Пусть сторона квадрата равна х,

тогда AM=12-x

BM=24-x

Δ АМК  подобен Δ КРВ  по двум углам ( один острый, второй прямой)

Из подобия

АМ:КР=МК:РВ

(12-х):х=х:(24-х)

Из пропорции получаем

x²=(12-x)(24-x)

x²=288-24x-12x+x²

36x=288

x=8

S( квадрата СМKP )=х²=8²=64

См. рис. 1

2.

S(полн)=S(осн)+S(бок)=π·r²+π·r·L

Если сторона равностороннего треугольника равна а, то высота

h=asqrt(3)/2 ⇒

a=2h/sqrt(3)=(2sqrt(3)/3)·h

a/2=(sqrt(3)/3)·h

r(фигуры вращения)=a/2

L=a

S(полн)=S(осн)+S(бок)=π·r²+π·r·L=π·r·(r+L)=π·(a/2)·((a/2)+a)=

=π·(a/2)·(3/2)·a=(3/4)π·a²=(3/4)·π·((2sqrt(3)/3)·h)²=π·h²=π·(19/π)=19

О т в е т. 19