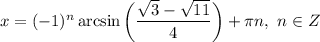Доброго времени суток, решить уравнение: 2cos²x = 1- (√3)*cos (3п/2+x)
Другие вопросы по теме Математика
Популярные вопросы
- Что нужно что бы продолжить существование людей на !...
1 - Составьте рассказ на тему культура 17 века быт...
2 - Решить систему уравнений {4х-3у=12 3х+4у=-24...
1 - (1/8+3/4)*16 (12 1/2: 2 1/2)-6 2: 2/3*1 1/2 3/4*5/7+3/4*2/7...
1 - Надо придумать тест 25 вопросов по россии. 5 вопросов- установите...
1 - Мне ! нужно составить сочинение словами из текста- старый дом,...
1 - 5. используя информацию из текста, выполни . выражение а^2 − a(a+...
2 - Нужно найти 10 вопросительных предложений и из этих предложений...
1 - Чем ластоногие схожи со всеми млекопитающими...
1 - Решите уравнение используя основное свойство пропорции (x-5): 16.2=2...
3
Замена:![\sin x = t, \ t \in [-1; \ 1]](/tpl/images/0295/6490/a1c18.png)
ответ: