Для заданной непрерывной случайной величины х:
1) записать и построить функцию плотности f(x);
2) записать и построить функцию распределения f(x);
3) проверить выполнение свойств f(x) и f(x);
4) найти характеристики: ожидание (m), дисперсию (d), среднее квадратичное отклонение (s), моду, медиану, коэффициент вариации, коэффициент ассиметрии, эксцесс;
5) найти p(|x –m| < s) и p(|x –m| < 3∙s). на график нанести m и интервалы, указанные в 5.
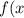=\left \{ {{1-\frac{a}{x^{2} } , x\geq1 } \atop {0, x\ \textless \ 1}} \right. \\a-? )
Другие вопросы по теме Математика
Популярные вопросы
- Мини конспект на тему Касымалы Баялинов...
2 - много ?#!#!#?#?]?]юыюыюыюыю...
1 - Знайти значення k,при якому вектори m (k;-8)і n(-4;-2...
2 - Цель восстания на Мангистау и Этапы восстания...
1 - Найдите ряд, в котором указаны черты публицистического стиля БЫСТРЕЕ...
3 - решите задачу в первом бидоне в 3 раза больше молока чем во втором.если...
3 - 4. (1 б) Розкладіть на множники: c2 + 10c + 25. A) (с + 5); Б) (с...
1 - Азия. Какие слова и выражения связаны с особенностями: а) рельефа;...
3 - нету больше последние отдавалЛучшие 2 ответа зделал и получил еще...
2 - Найди наиб значение функции у=4х2 на отрезке (-1:0) !...
3
1) Записать и построить функцию плотности f(x)
Заданная функция плотности f(x) выглядит следующим образом:
[f(x)= {{1-\frac{a}{x^{2}}}, x≥1
{0, x < 1}}]
Здесь a - неизвестная константа. Для построения функции плотности нужно определить значение a. Чтобы это сделать, воспользуемся свойством нормировки. Функция плотности должна удовлетворять следующему условию:
∫[1,+∞] f(x) dx = 1
Вычислим интеграл:
∫[1,+∞] (1 - a/x^2) dx = 1
Для удобства проведения вычислений заменим a/x^2 на t:
∫[1,+∞] (1 - t) dx = 1
∫[1,+∞] (1 - t) dx = x - tx^(-1)|[1,+∞] = (x - a/x)|[1,+∞] = (+∞ - a/∞) - (1 - a/1) = ∞ - 0 -1 + a = ∞ - 1 + a
Значит, ∞ - 1 + a = 1
a = 1
Таким образом, a = 1.
Функция плотности f(x) принимает следующий вид:
f(x) = {{1 - \frac{1}{x^{2}}}, x ≥ 1
{0, x < 1}}
Теперь построим график функции плотности.
2) Записать и построить функцию распределения F(x)
Функция распределения F(x) определяется как интеграл от функции плотности:
F(x) = ∫[1,x] f(t) dt
Для x ≥ 1:
F(x) = ∫[1,x] (1 - \frac{1}{t^{2}}) dt = t + \frac{1}{t}|[1,x] = (x + \frac{1}{x}) - (1 + \frac{1}{1}) = x - 1 + \frac{1}{x} - 1 = x - \frac{1}{x}
Для x < 1:
F(x) = ∫[1,x] 0 dt = 0
Теперь построим график функции распределения.
3) Проверить выполнение свойств f(x) и F(x)
Свойства функции плотности f(x):
- f(x) ≥ 0 для всех x
- ∫[-∞,+∞] f(x) dx = 1
Свойства функции распределения F(x):
- F(x) ≥ 0 для всех x
- F'(x) = f(x), где F'(x) - производная функции распределения
4) Найти характеристики: ожидание (m), дисперсию (d), среднее квадратичное отклонение (s), моду, медиану, коэффициент вариации, коэффициент ассиметрии, эксцесс
Для нахождения характеристик случайной величины, нужно вычислить определенные интегралы по функции плотности f(x).
Ожидание (m) = ∫[-∞,+∞] x*f(x) dx
Дисперсия (d) = ∫[-∞,+∞] (x - m)^2 * f(x) dx
Среднее квадратичное отклонение (s) = √(d)
Мода - значение x, при котором f(x) достигает максимума
Медиана - значение x, при котором F(x) = 0.5
Коэффициент вариации = s/m
Коэффициент ассиметрии = ∫[-∞,+∞] ((x - m)/s)^3 * f(x) dx
Эксцесс = ∫[-∞,+∞] ((x - m)/s)^4 * f(x) dx - 3
Вычислим эти характеристики по формулам для заданной функции плотности.
5) Найти P(|x – m| < s) и P(|x – m| < 3∙s) на графике нанести m и интервалы, указанные в 5.
P(|x - m| < s) = F(m+s) - F(m-s)
P(|x - m| < 3∙s) = F(m+3s) - F(m-3s)
Теперь вычислим эти вероятности и построим график с указанными интервалами на оси x.
Данный ответ представляет один из способов решения данной задачи. При решении могут быть использованы и другие методы.