Для произвольных вещественных a,b,c докажите неравенство

danilp7 2 17.08.2021 12:47 2

Question

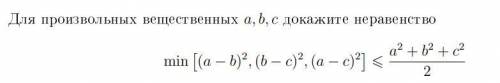
Математика: Для произвольных вещественных a,b,c докажите неравенство

danilp7 · Answer

Предположим, что a≤b≤c, причем расстояние между a и b не больше, чем между b и c (если бы расстояние между a и b было больше, мы могли бы умножить все три числа на минус 1, и тогда самым маленьким стало левое расстояние). Итак, мы имеем:

a=b-p; c=b+q; q≥p≥0. Надо доказать, что

2p²≤a²+b²+c², то есть 2p²≤(b-p)²+b²+(b+q)²;

2p²≤b²-2bp+p²+b²+b²+2bq+q²; 3b²+2b(q-p)+(q²-p²)≥0.

Заметим, что это квадратный трехчлен относительно b.

Поскольку старший коэффициент положителен, а дискриминант

D=4((q-p)^2-3(q^2-p^2))=4(q-p)(q-p-3q-3p)=-8(q-p)(q+2p)