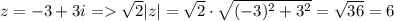Для комплексного числа z найдите 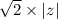
Корень квадратный из 2 × модуль Z
Eсли
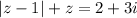
Другие вопросы по теме Математика
Популярные вопросы
- , заранее . Бригада гроз за месяц добыла 21 300 т угля. Комплексная...
2 - Відповіді на тести з географії 7 клас ст 190-191 ів...
1 - Нужна . Нужно написать рассказ с этих слов, чтобы все слова использовались...
3 - 3.Ех11 - page 85 Представьте ситуацию с двумя людьми, которые...
3 - 1. Направление в искусстве, следовавшее сложившимся канонам искусства...
1 - Произведение Ветер и солнце - это... Сказка Рассказ произведение...
2 - Найдите ошибки в предложениях. Определите, где при употреблении...
2 - Рассмотрите иллюстрацию к сказке Г.Х.Андерсена «Снежная королева»....
3 - 2 и 3 хелп английский язык 2 и 3 хелп ...
2 - Те Дати назви вуглеводням:CH3 -CE CHСН3 – CH = C-CH,- CHз / CH3CH-CE...
2
6
Пошаговое объяснение:
Пусть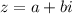 . Тогда
. Тогда 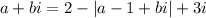
Два комплексных числа равны, если соответственно равны их действительные и мнимые части:
Для решения иррационального уравнения возведем обе части уравнения в квадрат с учетом неотрицательности правой части:
Значит,