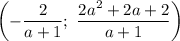Для каждого параметра решите систему уравнения a²x+y=2
x+y=2a
Другие вопросы по теме Математика
Популярные вопросы
- На первой полке было 9 книг,а на второй-8 книг,7 книг взяли.сколько книг...
2 - Укажiть речення ,у якому присудок э складеним дiэслiвним: а.снаряди почали...
3 - Слово поля и степи склонять по падежам. нужно. 4 класс. буду кто сделает...
2 - Какие однокоренные слова, отвечающие на вопрос кто или что, к слову выплюнул...
1 - Известно, что ctg(п/2-альфа)=-3 и альфа принадлежит (п/2; п). найдите cos...
3 - Бутылки с водой поставили в ящик,что получилось 4 ряда по 6 бутылок. сколько...
2 - Спиши, вставляя пропущенные буквы, расставляя знаки препинания.графически...
3 - Напишите сочинение на тему ,,люблю ли я зиму примерно 15 ! !...
2 - )1. -н- и -нн- в наречиях.(5 слов) 2. -н- и -нн- в краткой форме причастия.(5...
3 - Вертолет поднялся в воздух и пролетел 900км со скоростью 300км/ч. сколько...
1
Из первого уравнения вычтем второе:
1. Если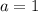 , то уравнение принимает вид:
, то уравнение принимает вид:
Решением данного уравнения является любое число.
Выражая из второго уравнения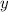 , получим соотношение:
, получим соотношение:
Подставим значение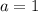 :
:
Подставляя вместо произвольное значение
произвольное значение 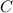 , поучим соответствующее значение
, поучим соответствующее значение  . Таким образом, решениями системы являются все пары чисел
. Таким образом, решениями системы являются все пары чисел 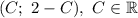 .
.
2. Если , то уравнение принимает вид:
, то уравнение принимает вид:
Полученное уравнение не имеет решений. Значит не имеет решений и система уравнений.
3. Если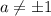 , то разделим обе части уравнения на
, то разделим обе части уравнения на  :
:
Выразим из второго уравнения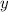 :
:
Подставим найденное значение :
:
при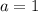 система имеет бесконечное множество решений вида
система имеет бесконечное множество решений вида 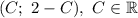
при система не имеет решений
система не имеет решений
при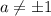 система имеет единственное решение
система имеет единственное решение