Для функции Z= f(x; у) найти:
а) полный дифференциал;
б) градиент функции Zв точке М (Xo;Yo);
в) производную функции z = f (x; у) в точке М (хо; Уo) по M направлению вектора а = {ax;ay}.
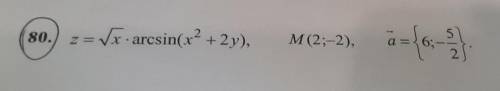
Другие вопросы по теме Математика
Популярные вопросы
- Теоретическая механика.Тело движется вниз по наклонной шероховатойплоскости,...
3 - В треугольнике, периметр которого 84 см, одна из сторон делится точкой...
3 - Как можно рассчитать тепловой эффект реакции: аА + bВ = сС + dD при Р,Т-сonst,...
1 - Два когерентных источника света с одинаковой начальной фазой образуют...
1 - 1.Анилинді өнеркәсіпте алу жолын ашқан ғалым: а) Н.Н.Зинин в) Ш.А.Вюрц...
3 - М. Горький. Пьеса « На дне». ответить на во письменно : Изображение правды...
3 - Люди , для чего нужны острые шипы на крышке маркера?...
3 - Укажите валентное состояние, типы гибридизации и типы связей(π, σ) атомов...
2 - За сколько минут автобус приезжает на остановку?,ну всмысле :приехал автобус...
2 - Відстань 160 км автомобіль подолав на 2 години швидше, ніж автобус. З...
2
а) Полный дифференциал функции Z = f(x, y) определяется следующим образом:
dZ = (∂Z/∂x)dx + (∂Z/∂y)dy,
где (∂Z/∂x) и (∂Z/∂y) - частные производные функции Z по переменным x и y соответственно, dx и dy - бесконечно малые приращения переменных x и y.
б) Градиент функции Z в точке М (Xo, Yo) определяется следующим образом:
grad Z = (∂Z/∂x)i + (∂Z/∂y)j,
где (∂Z/∂x) и (∂Z/∂y) - частные производные функции Z по переменным x и y соответственно, i и j - единичные векторы координатных осей.
в) Производная функции Z = f(x, y) в точке М (хо, Уо) по M направлению вектора а = {ax,ay} определяется формулой:
dZ/dM = (∂Z/∂x)(ax/∂x) + (∂Z/∂y)(ay/∂y),
где (∂Z/∂x) и (∂Z/∂y) - частные производные функции Z по переменным x и y соответственно, (ax/∂x) и (ay/∂y) - проекции вектора а = {ax,ay} на соответствующие производные.
Теперь разберемся с конкретной задачей:
В данной задаче нам дана функция Z = f(x, y), а также изображен ее график на рисунке. Обратимся к рисунку для более удобного определения значений переменных x и y в точке М (Xo, Yo) и проекций вектора а = {ax,ay}.
Для нахождения полного дифференциала функции Z (пункт а) необходимо вычислить частные производные по переменным x и y и подставить их значения в формулу полного дифференциала:
dZ = (∂Z/∂x)dx + (∂Z/∂y)dy.
Без конкретных численных значений функции Z и переменных x, y невозможно дать точный ответ на этот пункт. Необходимо использовать изображенный график функции для приближенного определения значений изменений dx и dy.
Для нахождения градиента функции Z в точке М (Xo, Yo) (пункт б) необходимо вычислить частные производные по переменным x и y и записать их значения в виде вектора:
grad Z = (∂Z/∂x)i + (∂Z/∂y)j.
Аналогично предыдущему пункту, без конкретных значений функции Z и переменных x, y невозможно дать точный ответ на этот пункт. Необходимо использовать изображенный график функции для приближенного определения значений частных производных и построения вектора градиента.
Для нахождения производной функции Z = f(x, y) в точке М (хо, Уо) по M направлению вектора а = {ax,ay} (пункт в) необходимо вычислить частные производные по переменным x и y, а также проекции вектора а = {ax,ay} на соответствующие производные и подставить их значения в формулу производной:
dZ/dM = (∂Z/∂x)(ax/∂x) + (∂Z/∂y)(ay/∂y).
Аналогично предыдущим пунктам, без конкретных значений функции Z и переменных x, y невозможно дать точный ответ на этот пункт. Необходимо использовать изображенный график функции для приближенного определения значений частных производных и проекций вектора а на эти производные.
Итак, чтобы решить данную задачу, необходимо использовать график функции Z = f(x, y) и приближенно определить значения dx, dy, частных производных и проекций вектора а. Затем подставить эти значения в соответствующие формулы для нахождения полного дифференциала, градиента и производной по направлению. В конечном итоге, получим численные значения ответов на каждый пункт задачи.