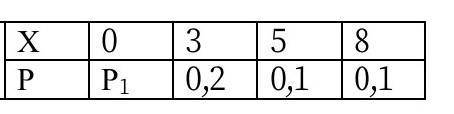
Для дискретной случайной величины Х, заданной рядом распределения, Найти:

а) P1

б)
интегральную функцию распределения, построить ее график;

в)
математическое ожидание, дисперсию, среднее квадратическое отклонение​

Для решения данной задачи, нам сначала необходимо понять, что представляет собой ряд распределения случайной величины X.

Ряд распределения показывает, какие значения может принимать случайная величина X и с какой вероятностью она принимает каждое из возможных значений.

В данной задаче ряд распределения представлен на изображении, где значения случайной величины X составляют множество {1, 2, 3, 4, 5}, а вероятности соответствующих значений заданы числами 0.1, 0.2, 0.3, 0.2 и 0.2 соответственно.

Теперь перейдем к решению поставленных вопросов:

а) Чтобы найти P1, необходимо найти вероятность P(X=1). Исходя из ряда распределения, мы видим, что P(X=1) = 0.1. Таким образом, P1 = 0.1.

б) Интегральная функция распределения (или функция распределения) для случайной величины X представляет собой функцию, которая показывает вероятность того, что случайная величина X примет значение меньше или равное определенного значения.

Для построения графика интегральной функции распределения, мы должны сначала рассчитать значения вероятностей суммируя вероятности значений случайной величины X, меньших или равных каждому из возможных значений.

Таким образом, значение функции распределения для X = 1 будет равно P(X ≤ 1) = P(X=1) = 0.1.
Для X = 2 значение функции распределения будет равно P(X ≤ 2) = P(X=1) + P(X=2) = 0.1 + 0.2 = 0.3.
Для X = 3 значение функции распределения будет равно P(X ≤ 3) = P(X=1) + P(X=2) + P(X=3) = 0.1 + 0.2 + 0.3 = 0.6.
Для X = 4 значение функции распределения будет равно P(X ≤ 4) = P(X=1) + P(X=2) + P(X=3) + P(X=4) = 0.1 + 0.2 + 0.3 + 0.2 = 0.8.
Для X = 5 значение функции распределения будет равно P(X ≤ 5) = P(X=1) + P(X=2) + P(X=3) + P(X=4) + P(X=5) = 0.1 + 0.2 + 0.3 + 0.2 + 0.2 = 1.

Теперь, чтобы построить график, мы отметим значения случайной величины X на оси абсцисс и значения функции распределения на оси ординат и соединим полученные точки прямыми.

в) Для нахождения математического ожидания (M), дисперсии (D) и среднего квадратического отклонения (σ), мы должны воспользоваться формулами:

M = ∑(xi * Pi) - где xi - значение случайной величины, Pi - вероятность значения xi
D = ∑((xi - M)^2 * Pi) - где xi - значение случайной величины, Pi - вероятность значения xi
σ = √D - среднее квадратическое отклонение

Рассчитаем математическое ожидание:
M = (1*0.1) + (2*0.2) + (3*0.3) + (4*0.2) + (5*0.2) = 1 + 0.4 + 0.9 + 0.8 + 1 = 4.1

Рассчитаем дисперсию:
D = ((1-4.1)^2 * 0.1) + ((2-4.1)^2 * 0.2) + ((3-4.1)^2 * 0.3) + ((4-4.1)^2 * 0.2) + ((5-4.1)^2 * 0.2) = 6.09 + 2.41 + 0.09 + 0.02 + 0.18 = 8.79

Рассчитаем среднее квадратическое отклонение:
σ = √D = √8.79 ≈ 2.96

Таким образом, математическое ожидание M = 4.1, дисперсия D = 8.79 и среднее квадратическое отклонение σ ≈ 2.96.