Для действительных a < b доказать неравенство:
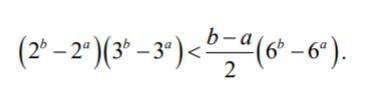
Другие вопросы по теме Математика
Популярные вопросы
- Мини сочинение на тему: частица не с прилагательными...
3 - Вопрос: как человек стал расселяться по земле? ответ: людям надо...
3 - Периметр равнобедренного треугольника равен 18 см.одна из его...
1 - Для оформления сцены купили по одной цене 37 метров белого и 42...
1 - Решите неравенство и изобразите множество его решений на координатной...
2 - Корова, сорока, медведь, заяц, воробей, яблоко, карандаш. подчеркни...
3 - Джони знакомиться с пришельцем из космоса и хочет узнать его имя...
1 - Какую информацию содержит карта полушарий...
2 - Длинна прямоугольника- 10 см а ширина 5 см какой периметр?...
1 - Используя знания систематики позвоночных животных, составьте схему,...
2
Пусть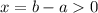 . Тогда:
. Тогда: 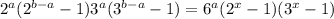 ,
, 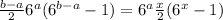 , возвращаясь к неравенству и сокращая на
, возвращаясь к неравенству и сокращая на 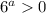 , получаем:
, получаем: 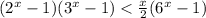 .
.
Рассмотрим две непрерывные одинаково выпуклые функции. Они могут пересекаться не более чем в одной точке. Действительно, пусть таких точек хотя бы две. Соединим соседние, тогда эта хорда для одной функции располагается над графиком, а для другой — под графиком. Значит, функции разной выпуклости. Следовательно, точек пересечения не более одной.
Легко проверить, что функции, стоящие в обеих частях являются выпуклыми вниз (достаточно дважды продифференцировать или просто раскрыть скобки, разбив функцию на элементарные составляющие).
Графики функции пересекаются в точке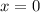 , значит, для
, значит, для 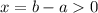 они больше нигде не пересекаются. Например, при
они больше нигде не пересекаются. Например, при 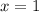 неравенство выполнено, стало быть, оно будет выполнено и для остальных положительных
неравенство выполнено, стало быть, оно будет выполнено и для остальных положительных  .
.